| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Perceptron
- TFRecord
- 블록체인
- error
- numpy
- opencv
- 유가 급등
- qtdesigner
- 브렉시트
- 딥러닝
- loss
- Python
- 세계사
- TF
- itksnap
- dtype
- img
- 유로화
- terminal
- deeplearning
- Training
- keras
- TensorFlow
- cv2
- DataSet
- Inference
- 세계대전
- 비트코인
- pyqt
- 퍼셉트론
- Today
- Total
활연개랑
[딥러닝] 딥러닝 기본 정리 해석 - 2 본문
딥러닝 기본 정리 해석 1편
https://tmdhhey.tistory.com/63
[딥러닝] 딥러닝 기본 정리 해석 - 1
http://neuralnetworksanddeeplearning.com/index.html Neural networks and deep learning neuralnetworksanddeeplearning.com 딥러닝의 기본에 대해 자세히 설명되어있는 사이트입니다. 공부할겸 차근차근 블로..
tmdhhey.tistory.com
Sigmoid neurons
학습 알고리즘은 정말 좋은 것 같습니다. 하지만 어떻게 신경망을 위한 학습 알고리즘을 고안해낼 수 있을까요?
퍼셉트론 네트워크가 있다고 가정해봅시다. 이 퍼셉트론 네트워크를 통해 문제를 해결하는 방법을 학습하고자 합니다.
예를들어 네트워크에 대한 입력은 손으로 쓴 숫자 이미지의 원시 픽셀 데이터라고 봅시다. 그리고 우리는 네트워크에서 가중치와 bias를 학습하여 네트워크로부터의 출력이 우리가 인식하듯이 정확하게 분류해내기를 원합니다. 학습이 작동하는 방식을 확인해보기 위해 네트워크에서 일부 가중치를 약간 변경한다고 가정합시다. 우리가 원하는 것은 이 작은 가중치의 변화가 네트워크로부터의 출력에 상응하는 작은 변화만을 야기하는 것입니다. 잠시 후 알게 되겠지만, 이 특성이 학습을 가능하게 할 것입니다. 아래 그림에 우리가 원하는 것이 있습니다. (사실 이 네트워크는 필기 인식을 하기에는 너무 간단합니다.)

가중치의 작은 변화가 출력에 작은 변화만 일으킨다는 것이 사실이라면, 이 사실을 이용해 가중치와 bias를 수정하여 우리가 원하는 방식으로 작동하는 네트워크를 만들 수 있을 것입니다. 예를들어, 네트워크가 이미지를 9를 8로 못 분류했다고 가정해봅시다. 우리는 네트워크가 이미지를 9로 분류하는데 조금 더 가까워지도록 가중치와 bias를 약간 변경하는 방법을 알아낼 수 있습니다. 그런 다음 더 나은 결과를 생성하기 위해 가중치와 편향을 계속해서 변경하면서 이 것을 반복애 더 나은 결과를 만들어낼 것입니다. 그렇게 네트워크는 학습할 것입니다.
문제는 우리의 네트워크가 퍼셉트론을 포함하게되면 이런 일이 일어나지 않는다는 것입니다. 사실, 네트워크에서 단일 퍼셉트론의 weight나 bias의 작은 변화는 때때로 퍼셉트론의 출력이 완전히 뒤집히게 될 수 있습니다. 이렇게 뒤집히게 되면 네트워크의 나머지 부분의 동작을 매우 복잡한 방식으로 완전히 변화시킬 수도 있습니다. 따라서 이제 9가 올바르게 분류 되었다고 해도 다른 모든 이미지 네트워크의 동작은 제어하기 어려운 방식으로 완전히 바뀌었을 수 있다는 의미입니다. 이는 네트워크가 우리가 원하는 방식으로 동작하도록 가중치와 bias를 점진적으로 수정하는 방법을 확인하기 어렵게 만듭니다. 아마도 이 문제를 해결할 수 있는 방법이 있을 것입니다.
우리는 시그모이드 뉴런이라고 불리는 새로운 형태의 인공 뉴런을 도입함으로써 이 문제를 극복할 수 있습니다. 시그모이드 뉴런은 퍼셉트론과 유사하지만 가중치와 편향의 작은 변화가 출력제 작은 변화만을 일으키도록 변형되었습니다. 그것이 시그모이드 뉴런의 네트워크가 학습할 수 있도록 하는 중요한 부분입니다.
시그모이드 뉴런에 대해 설명하겠습니다. 우리는 아래처럼 퍼셉트론을 묘사한 것과 같은 방식으로 시그모이드 뉴런을 묘사할 것입니다.

퍼셉트론처럼 시그모이드 뉴런은 x1,x2...의 입력을 가지고 있습니다. 예를들어 0.638은 시그모이드 뉴런에 유효한 입력입니다. 또한 퍼셉트론과 같이 시그모이드 뉴런은 각 입력에 대한 가중치 w1,w2... 와 전체적인 편향 b를 갖고있습니다. 하지만 출력은 0이나 1이 아닙니다. 대신 σ(w⋅x+b) 공식이 되고 여기서 σ는 시그모이드 함수라고 불립니다
**동시에 σ는 때때로 로지스틱 함수라고 불리며, 이 새로운 뉴런의 부류는 로지스틱 뉴런이라고 불립니다. 이 용어들은 신경망을 연구하는 많은 사람들에 의해 사용되기 때문에 기억해두는 것이 좋습니다. 그러나 우리는 시그모이드 용어로 σ를 사용할 것이며, 다음과 같이 정의됩니다.
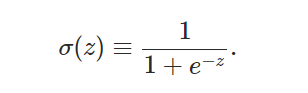
여기에서 추가로 입력 x1,x2....과 가중치 w1,w2...그리고 바이어스 b를 가진 시그모이드 뉴런의 출력은 다음과 같습니다.

딱 볼 때 시그모이드 뉴런은 퍼셉트론과 매우 달리 보입니다. 시그모이드 함수의 대수적 형식은 아직 익숙하지 않은 경우 어렵게 보일 수 있습니다. 사실 퍼셉트론과 시그모이드 뉴런 사이에는 많은 유사점이 있으며, 시그모이드 함수의 대수적 형태는 이해해 대한 장벽이라기보다 기술적인 세부사항에 더 가깝습니다.
퍼셉트론 모델과의 유사점을 이해하기 위해 다음과 같이 가정합니다. z≡w⋅x+b 는 큰 양수입니다. 그 다음에 e^(-z)≈0 이고 σ(z)≈1가 됩니다. 다시 말하면, z=w⋅x+b가 크고 양수라면, 시그모이드 뉴런 출력은 퍼셉트론 처럼 대략 1이다.
반면에, z=w⋅x+b가 완전 음수라고 가정합시다. 그러면 e^(-z)→∞ 그리고 σ(z)≈0가 됩니다. 따라서 z=w⋅x+b가 매우 음수라면, 시그모이드 뉴런 또한 퍼셉트론에 가깝습니다. w⋅x+b가 적당한 크기일 때에만 퍼셉트론 모델과 많은 편차가 있습니다.
σ의 대수적 의미는 무엇일까? 어떻게 그것을 이해할 수 있을까요? 사실 σ의 정확한 형태는 그렇게 중요하지 않습니다. 실제로 중요한 것은 함수 모양입니다.


만약 σ가 실제로 계단함수였다면, 출력은 다음과 같으므로 S자형 뉴런은 퍼셉트론이 됩니다. 출력은 w⋅x+b가 양수인지 음수인지에 따라 1 또는 0이 되기 때문입니다. 위에서 암시된 것처럼 실제 σ함수를 사용함으로써 퍼셉트론을 평활하게 만들 수 있습니다. 실제로 중요한 것은 σ함수의 부드러운 형태이지 이것의 디테일한 부분이 아닙니다.
σ의 부드러움은 가중치의 작은 변화 Δw_{j}와 bias Δb가 뉴런의 출력에서 작은 변화 Δoutput을 생성한다는 것입니다.
사실, 미적분학은 우리에게 Δoutput이 다음을과 근사하다고 말한다.
만약 γ가 실제로 단계 함수였다면, 시그모이드 뉴런은 퍼셉트론일 것이다. 위에 이미 암시된 것처럼 실제 γ 함수를 사용함으로써 퍼셉트론을 평활하게 만들 수 있습니다. 실제로 중요한 것은 form 함수의 부드러움이지 상세한 형태가 아니다. γ의 부드러움은 무게의 작은 변화 Δw_{j}와 바이어스의 Δb가 뉴런의 출력에서 작은 변화 Δ를 생성한다는 것을 의미한다. 사실, 미적분학은 우리에게 "출력"이 잘 대략적으로 표현된다고 말한다.

나중에 또 적으러올게요
'딥러닝' 카테고리의 다른 글
| [deeplearning] PSNR 사용목적 및 의미 (0) | 2022.05.18 |
|---|---|
| [Computer Vision] gaussian filter (가우시안 필터) 사용 이유 - mean filter와의 차이점 (0) | 2022.05.18 |
| [딥러닝] 딥러닝 기본 정리 해석 - 1 (0) | 2022.02.01 |
| 수학기호,단위 정리 +발음 (0) | 2022.01.12 |
| [deeplearning(딥러닝)] 경사하강법(gradient decent) (0) | 2021.12.26 |





