딥러닝/알아두면 좋을 지식
[Frequency] Haar wavelet transformation
승해tmdhey
2025. 4. 15. 03:20
반응형
Haar Wavelet이란?
- 최초의 웨이블릿(1910년)
- 매우 단순한 형태의 계단 함수(step function)
- 한 구간에서 +1, 그 다음 구간에서 -1
수식적 정의:
- 기본 Haar 함수 (mother wavelet)

- 여기서 (1, 0)은
- a = 1 → 스케일(크기)
- b = 0 → 위치(시간 이동)
(a, b) 파라미터 의미
| a (scale) | 얼마나 wavelet을 압축/확대할지 | 작을수록 더 좁고 세밀해짐 |
| b (shift) | wavelet을 시간축에서 얼마나 이동시킬지 | 오른쪽으로 움직일수록 더 뒤에 위치함 |
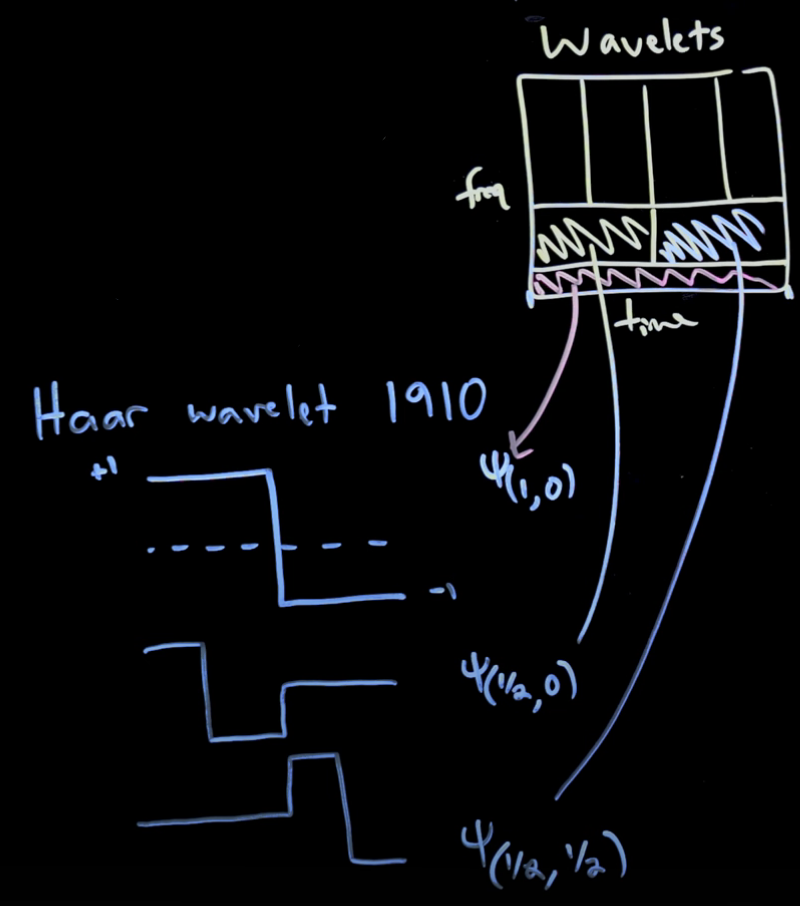

- : 전체 구간에 대한 큰 구조

- 왼쪽 절반 구간의 구조

- 오른쪽 절반 구간의 구조
→ 그림에서 세 파형이 바로 이걸 시각화하고 있음.
이걸 왜 쓰는가?
직관
- 큰 스케일(a=1)은 큰 구조 (예: 이미지 전체 밝기 변화)
- 작은 스케일(a=1/2, 1/4...)은 작은 구조 (예: 경계, 윤곽, 눈, 입 등)
활용
- Wavelet 변환은 신호를 \psi_{a,b}(t)들로 투영하여
각 스케일/위치별 "얼마나 잘 맞는지" (내적 값) 계산
→ → 이것이 Wavelet Transform
직교성 (Orthogonality)
- 서로 다른 wavelet들은 내적이 0

- 이유:
- 한 wavelet이 +1일 때, 다른 건 +1/−1로 반반 존재 → 합이 0
- 이 성질 덕분에 모든 신호를 안정적으로 분해 가능
해석>다중해상도 분석
스케일해석 범위해상도분석 특징
| 큰 스케일 (a=1) | 전체 구간 | 저해상도 | 큰 구조만 파악 |
| 중간 스케일 (a=1/2) | 절반 구간 | 중간 해상도 | 중간 크기 구조 |
| 작은 스케일 (a=1/4, ...) | 세부 구간 | 고해상도 | 세밀한 엣지나 변화 감지 |
→ 그림 오른쪽 위의 Time-Frequency 박스에서
→ 높은 freq 구간일수록 짧은 시간 구간에만 wavelet이 존재하는 걸 볼 수 있음.
핵심 요약
- Haar wavelet은 가장 간단하고 직관적인 wavelet
- (a, b) 조절로 다양한 시간/주파수 해상도 확보 가능
- 큰 구조는 긴 wavelet, 작은 세부는 짧은 wavelet
- 내적 결과가 wavelet transform 결과
- 이미지/오디오/시계열 모두 분석 가능